Karmasik kompleks sayilar nedir tanimi toplama cikarma carpma bolme islemi konu anlatimi grafik gosterimi-Haber Keyfim

Cuma

Karmasik kompleks sayilar nedir tanimi toplama cikarma carpma bolme islemi konu anlatimi grafik gosterimi

KARMAŞIK SAYILAR VE KOMPLEKS SAYILAR NE DEMEKTİR?

Karmaşık sayılar, gerçel sayıların bir genişlemesidir ve $mathbb{C}$ ile gösterilir. Karmaşık sayılar kümesi, gerçel sayılar kümesini kapsar. Karmaşık sayılar biri gerçel biri sanal olmak üzere iki kısımdan oluşur. Bütün karmaşık sayılar a ve b birer gerçel sayı olmak üzere, a + bi biçimde yazılabilir. Burada i, x² = - 1

denkleminin köklerinden biri, başka bir deyişle -1′in kareköküdür. Kimi zaman özellikle elektrik mühendisliğinde i yerine, j kullanılır.

Karmaşık sayılarda işlemler nasıl yapılır?

Toplama ve çıkarma

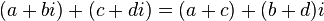
$( a + bi ) + ( c + di ) = ( a + c ) + ( b + d )i ,$
$( a + bi ) - ( c + di ) = ( a - c ) + ( b - d )i,$

Çarpma

$( a + bi ) cdot ( c + d i) = ac - bd + ( bc + ad ),i ,$

Bölme

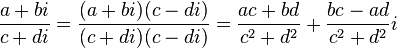
$frac{ a + bi }{ c + di } = frac{(a + bi ) ( c - di )}{( c + d i) ( c - di)} = frac{ ac + bd }{ c^2 + d^2 } + frac{ bc - ad }{ c^2 + d^2 }i$
Diğer bir ifade yöntemiyle şu şekilde yazılır.
$zinmathbb{C}$ olmak üzere; z = (a,b) = a + bi Buradan da anlaşılabileceği gibi Re(z) = a ve Im(z) = b dir.
Toplama ve çarpma işlemi ise şu şekilde tanımlanır: z₁ = (a,b),z₂ = (c,d) olmak üzere;
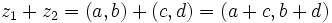
$z_1 + z_2 = (a,b) + (c,d) = (a+c,b+d) ,$
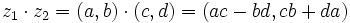
$z_1 cdot z_2 = (a,b) cdot (c,d) = (ac-bd,cb+da) ,$
Bu sonuçtan yukarıdaki eşitlikleri çıkartabiliriz.